100%成功率的顶象面积验证码识别方案
写在最前面:
本文只会讲思路,不会放代码,不会放代码,不会放代码,重要的事情说三遍。
因为这个事情还是比较敏感的,顶象在验证码方向做的也算是比较大的了,国内很多公司在用的验证码都是顶象的,代码就不放了,避免被人拿去做坏事了。
另外,也是为顶象的验证码做个简单的测试。如果有顶象的大佬看到,可以考虑把这个验证码更新一下啦~
纯一时手痒,仅为技术交流,请勿用于任何商业活动,也请勿对顶象的验证码进行攻击,感谢~
请不要进行任何违法行为,否则后果自负!
以下正文。
前两天有位大佬丢过来一张验证码图片,问我该如何处理。验证码它长这样,要求是点击图片中被分割出来的最大的区域:

哟吼,这验证码,有点东西啊~
但是大佬问的问题,说什么也得给搞定嘛~
于是,我思索了一下,一个想法慢慢成形,我觉得可以把任务拆解成几个小问题:
- 1.检测出图片中被标记出来的点
- 2.将检测出来的点连成一条线
- 3.根据线将图像切割成几个不连通的区域
- 4.计算各个区域的面积,获取面积最大的区域的一个点的坐标,即为结果
略微推敲了几遍,觉得想法可行,于是,开搞~
转载请注明来源:https://blog.csdn.net/aaronjny/article/details/110245896
一、检测出图片中被标记出来的点
先来解决第一个问题,怎么检测出图片中被标记出来的点。
我最直接的想法是使用目标检测算法,因为这些点还是挺明显的,目标检测模型(比如yolo)应该是可以奏效的。但是一张图片上的点比较多,标注数据集感觉很麻烦,虽然觉得可行,但真心不想费那么大功夫。
又看到标记点的颜色和正常图片的颜色还是有一定差别的,于是,我决定先尝试直接在图片的像素和色值上下些功夫。
1、BGR图像上的、基于离群值筛选的检测方法
考虑到标记点和正常图片的颜色上的差别,可以初步判断一个标记点和周围的其他像素点在色值上是有一定偏离的,我们可以考虑把色值与相邻局部区域整体色值有一定大小偏离的点,认为是标记点。
emmm,话比较绕是吧?感觉不太好理解?那我来举个例子:
有一只哈士奇混在了一群狼里面,虽然都是犬科,但是长得还是不太一样的,我们需要把二哈揪出来~

我们以前面的示例图片为例,解释一下这个问题,请看:

以蓝色框圈起来的绿色点群(实际上是很多绿色点聚在一起了,不只是一个点)为例,在蓝色框选中的图片区域里可以看到,虽然已经有不少绿色点了,但这个点的数量占蓝色框里的全部点的比例还是偏少的,更多的是正常的点。
假如说把蓝色框扩大,变成红色框,会发现,虽然绿色点数量增加了,但正常点的数量增加的更多,绿色点的比例进一步降低了。
那么,相对于正常点来说,标记点的色值就是离群值了(偏离了周围正常点的色值范围)。那么,我们就可以先设定一个框框,然后滑动这个窗口,遍历整张图片,计算窗口在每个位置检测出离群值的点,这些点就可以作为标记点。
那么,具体该怎么做呢?
其实检测离群点的算法有很多,我这里介绍一种,绝对中位差法。
①对于一个h*w的矩阵M,先统计其中位数,即为median。
②对于矩阵M中的每一个值,都是用它减去 median,并取绝对值,获得新的矩阵N。
③对N求中位数,即中位差,我们记为mad。
④我们认为在区间 [median-x*mad,median+x*mad] 内的点属于正常点,超出则为离群点,x看情况设置,我们这里取3。
如果使用 numpy 来描述这个过程的话,如果要检测点(row,col)是否为离群值,可以表示如下:
- 1
有几点要注意的是:
- 1.这里的矩阵M实际上并不是整张图片,按前面的描述应该也能看出来,M指的实际上是要检测点(row,col)向周围等距离扩散出来的一个小矩阵。
- 2.我这里也只是针对矩阵举例的,实际上BGR图片是(h,w,3)的,而不是(h,w)的,所以这里实际处理的时候是分别对3个图像信道做了绝对中位差法筛选(即调用3次,每次处理一个信道,均在正常范围内才认为是正常点)。
如果还不明白的话,我再举个具体的例子,我随便编了一个小矩阵,5*9的,如下图蓝色框所示:

假设我们取影响距离k为1(表示只关注距离待检测点不超过1个格子的点),那么滑动窗口(感受野)的大小就是1*2+1=3。假设我们要检测的点时第3行第3列的点,则窗口可以用红色框表示:

还记得中位数是什么吗?把一组数按照从小到大的顺序排列,最中间的数就是中位数。对于这个红色框来说,从小到大排列为:
- 1
一共9个数,最中间的数是第5个,数值是2,即 median = 2。
然后计算出矩阵N,即让矩阵M(红色框)中的每个数都减去 median ,并取绝对值 :
2
3
4
5
然后计算N的中位数,[0,0,0,0,1,1,2,2,3],得到 mad=1。
根据 [median-x*mad,median+x*mad],当x取3时,可以计算出正常区间为[2-3*1,2+3*1],即[-1,5]。第3行第3列的数字刚好为3,在这个区间里,不是离群值。
接着我们判断第3行第4列的数字是否为离群值:
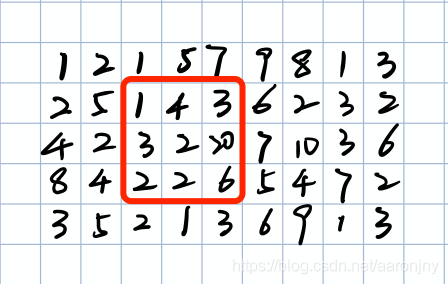
简单计算一下:
第3行第4列的数字2在这个区间里,是正常值。
再将窗口右移一格:

计算一下:
1
2
3
4
5
6
第3行第5列数值为20,不在这个区间里,为异常值。这个和我们的直观判断也是一致的,因为20确实比旁边的数都大很多,属于异常值。
这样应该明白了吧?
OK,我们使用绝对中位差法测试一下,检测效果一般,如下图所示:

可以看到,虽然标记点被检测出来了(事实证明是这一张相对容易检测,在其他的样本上还会存在部分标记点没有被检测出来的情况),但也误将一些正常的点识别为了标记点,我们把这些误识别的点称为噪声,因为它们相对于我们要检测的标记点来说,就是一种干扰。
那么,我们需要进行降噪。
降噪的方法也很简单,跟上面的方法类似。我也是取一个局部的窗口,统计窗口内被认为是标记点的个数,以及窗口内全部点的个数(即被认为是正常的点+被认为是标记点的点),计算占比。从图片上可以看出,噪声一般是比较零散的,所以可以通过占比阈值的设置过滤掉大部分噪声点。
降噪后的结果如下:

结果确实好了很多,可以看到大部分噪点被过滤掉了,只剩下小部分比较密集的还在负隅顽抗。但同时也能看到,这种降噪方法也会对识别正确的标记点产生负面影响(即把正确的标记点也认为是噪点了,虽然很少,但在上图还是能看到的),所以关于阈值的设置需要好好权衡。
还有一点需要注意的是,对于每个点都做绝对中位差法检测的话,计算量还是太大了,消耗的时间比较高。
多给几个示例,就能够看出检测结果不够好了:


2、灰度图像上、基于离群值筛选的检测方法
我们已经在BGR图像上进行了离群值筛选,那么可以考虑一下,我能否直接在灰度图像上这么做?
毕竟一来,BGR有3个信道,灰度图片只有1个信道,所以本来需要做3次的运算现在只用做1次了,计算量能有较大幅度的降低;二来,说不定只从灰度明暗的角度处理,效果会更好?
于是,我将图片转灰度,再做测试。图片转灰度:

使用绝对中位差法检测标记点:

过滤噪声点:

可以看到,速度和效果均略微提升,但提升有限。
再多给几个示例对比:
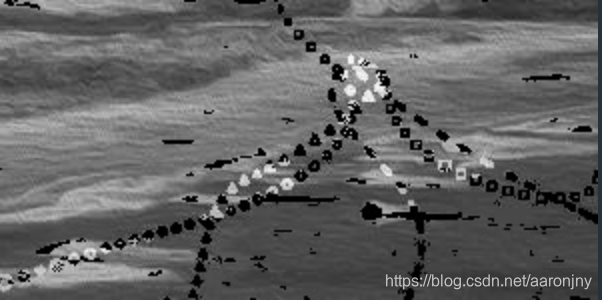

另外,转灰度之后能够看到,标记点整体是比正常点偏亮一点的。所以也可以尝试直接设置色值的阈值,来检测标记点。经测试,速度会更快,但效果比绝对中位差法要差一些,所以我就不再展开了。
3、哈里斯角点检测
如果觉得绝对中位差在处理这个任务时还是不够好的话,有什么更好的方法吗?
有的!从朋友那里得知哈里斯角点检测算法时,我整个人都惊呆了——竟然还有这么牛X的算法?

这是什么神仙算法?
处理验证码简直不要太好用好不好?
为自己狭窄的知识面默哀……在线卑微……

那么,什么是哈里斯角点检测呢?
要说哈里斯角点检测,得先说一下角点。
那么,什么是角点呢?
角点可以简单理解为是两条边的交点。可以类比我们的桌角、笔尖等,如果将桌子和笔拍下来,桌角和笔尖都会是角点。
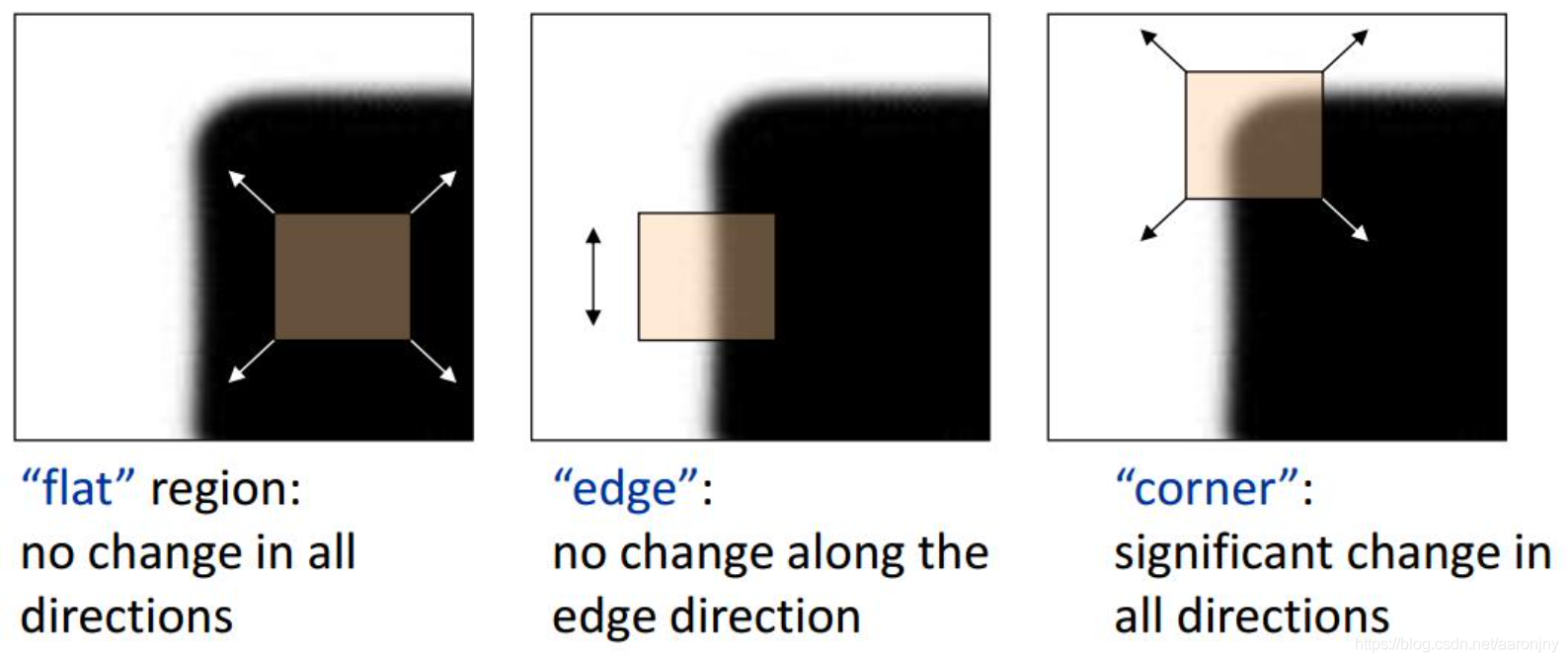
上面的定义是为了方便我们理解的,如果严格一点来说的话,角点指的是在邻域内具有两个(及以上)主方向的特征点。它在图像中有具体的坐标和某些数学特征,通常表现为:
轮廓之间的交点
对于同一场景,即使视角发生变化,通常具备稳定性质的特征
该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化
如下图所示,在各个方向上移动小窗口,如果在所有方向上移动,窗口内灰度都发生变化,则认为是角点;如果任何方向都不变化,则是均匀区域;如果灰度只在一个方向上变化,则可能是图像边缘。
哈里斯角点检测的基本思想是什么呢?
算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么我们可以认为该窗口中存在角点。
以上关于哈里斯角点检测的内容,主要整理、参考于下面两篇文章,感兴趣的话可以阅读一下:
- Harris角点检测原理详解 (https://blog.csdn.net/lwzkiller/article/details/54633670)
- 图像特征之Harris角点检测 (https://senitco.github.io/2017/06/18/image-feature-harris/)
好了,问题又来了——哈里斯角点检测算法实现困难吗?
不用担心,opencv 已经帮你实现好啦~ 调用cv2.cornerHarris 即可。
那哈里斯角点检测的效果如何呢?仍然选取初次测试的图片,看下效果:

哟呵,效果很不错哦~虽然有小部分标记点没检测出来,但大体轮廓已经在了,而且关键是,几乎没有噪点,这对我们后面的处理提供了极大的便利。
还有一个明显的优点是,哈里斯角点检测的速度很快,再加上检测效果不错,降噪部分的代码也可以去掉了,计算速度有了明显的提升。
多给几个示例对比:


我觉得效果已经很不错了,那标记点的检测就到这里吧?可以开始下一步了。
二、将检测出来的点连成一条线
关于如何将点连成一条线这件事上,我也想了两种方法:
- 使用图搜索,将标记点组成连通域,再搜索域和域之间的最短路径,当距离不超过一定值时进行连接。反复迭代这个过程,直到所有的域都不能再连通或者只剩下了一个域
- 直接将每一个原始被标记点周围一定范围内的点,都也变成被标记点,我把这个过程称为“浸染”。其中,只有原始的被标记点有浸染能力,被浸染出来的被标记点不具备二次浸染周围点的能力。这样相当于把每个标记点都放大了,只要点足够大,点与点之间的缝隙也就被点本身给覆盖掉了,也就连成了线。
第一种方法的效果确实不错,我觉得主要有两个缺点:
- 算法写起来麻烦
- 时间复杂度特别特别特别高
第一个缺点对我来说问题不算大,我已经写好了。但第二个缺点就严重影响实用了,没法在工程里面用起来,遂放弃。
第二种方法虽然简单粗暴,但快速有效啊。可能有的同学会疑惑,如果我对被标记点进行浸染的话,最终被标记点的数量会变多,会占用原来的正常点,这样是不是会对我最后计算面积产生影响啊?
影响肯定是有点,这样连线分割之后的区域,面积算起来肯定比正常的要小。但我只需要判断哪个区域更大就行了,并不需要我精准返回面积(不说算法了,人也没法判断出来啊),我这么做并不会改变各区域的面积大小顺序,所以并无大碍。
浸染的时候,还要考虑浸染多大范围。当浸染的范围是0时(即不浸染周围的元素),就和第一步的检测结果一致:

当浸染范围是1时(即影响周围距离不超过1的格子,实际表现就是以当前点为中心的一个3*3的窗口),连线结果为:

浸染范围为2时(5*5的窗口):

需要注意的是,浸染也是有一定计算量的。当浸染范围越大(但也不能太大,不然可能会把线都糊在一起)时,对区域的划分就越精确,越不容易出现连线里有断点的情况,但耗时也会越大。
我最终将阈值设在了7,能够在保证精度的同时兼顾性能:

再多看两个例子:


连线做到这一步也就可以了,开始下一步。
三、根据线将图像切割成几个不连通的区域
我们以这张图片为例:

我们要做的是,让程序能将图片里面的五个区域给识别区分出来:

具体该怎么做呢——兄dei,你听说过深度优先搜索吗?
其实这就是一个简单的图搜索问题,搜索出图中所有连通的像素,每一个连通域就是一个切割出来的区域。
如果你还不理解的话,我们可以这么看:
首先,你有一张图:

然后,从左上角出发,也就是坐标(0,0)的位置。如果它不是黑色的被标记点,就将它涂成红色。

然后从这个点开始向外扩散,把遇到的所有不是黑色的标记点都涂成红色。



注意,在涂的过程中,你还需要记录下你涂过的点的坐标。现在这个区域被涂满了,无法再继续了,而你也已获得了一个连通域(包括这个域里的点的坐标集),也就是一个分割出来的子图。
接下来,我们再逐行扫描这张图,找到第一个不是红色、也不是黑色的点,我们就找到了下面这个紫色的点:

然后跟上面的步骤相同,逐步扩散,直到不能再扩散为止:

这样,我们又获得了第二个连通域,也就是第二个切割出来的子图。
使用同样的方式,我们能够获得剩下的三个连通域,也就是如下的黄、绿、蓝三个区域:
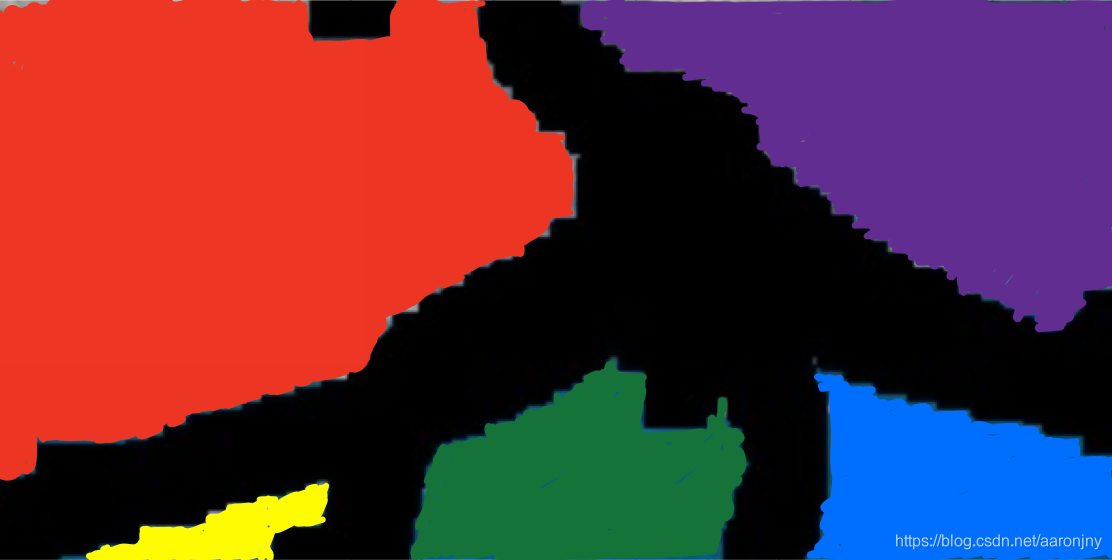
你看,这不是很轻松就完成了子图的分割吗?
编码上也并不困难,只要会写递归,再简单学习一下图搜索相关的算法,就能够写出来,很简单的。而且流程我已经说的很细了,按照我说的流程直接实现也是没问题的。我刚才已经对连通域搜索算法做了详细的举例,这要是还搞不明白的话我也没办法啦~
当然了,上面是为了理解起来方便一点,讲的比较细致繁琐,实际开发中某些流程是可以被优化的。
四、计算各个区域的面积,获取面积最大的区域的一个点的坐标,即为结果
在上一步,我们已经获得了所有连通子图,以及它们对应的点集。
再来回顾一下验证码需要我们做的——点击面积最大的子图。
把问题拆的细一点,如下:
- 计算各个子图的面积
- 找出面积最大的子图
- 获取该子图中的随机一个点的坐标
①怎么计算面积?
最简单的方法,统计子图里面点的数量不就可以吗?类似于积分的思想。我们已经获得了每个子图对应的点集,所以这一步就只是简单的统计,很容易做到。
②怎么找出面积最大的子图?
这个就不用说了吧?排个序就行了嘛。
③怎么获取该子图中随机的一个点的坐标?
emmm,爱怎么获取怎么获取呗,用 python 的 random 标准库随机选一个也行,嫌麻烦的话,直接去点集里面的第一个点也行,只要保证属于面积最大的子图的点集就行。
五、结果展示
所有的流程都走完了,不妨选几张图片做个测试。我手里总共有10张样例图片(蓝色点是要点击的地方)。


对于上面这张图片,可以发现,蓝色点竟然和黑色点重叠了?
其实是没有问题的。为了展示的清楚,我把蓝色点也放大了很多倍,原始的点(要点击的坐标)实际上是和黑色点无重叠的。
另外,我将黑色点浸染得很粗,本身就也相当于做了一定的冗余,也能保证不会出现点击在标记点上的情况。
继续看:








可以看到效果还不错哈~我们下面来做结果分析。
六、结果分析
从刚开始开发,到最后完成,我经历了几个版本的迭代优化。
①第一个版本,是研究可行性的代码。
实现思路:
BGR图像上的绝对中位差法 + 降噪 + 标记点浸染连线 + 图连通搜索
这个版本只是为了验证思路是否可行,各方面没做什么优化,所以执行效率比较低,工程阶段基本没法用。
执行时间:
1分钟
通过率:
一般
②第二个版本是对第一个版本的改进,主要使用了numpy和各种提速技巧对算法做了性能优化。
实现思路:
- BGR图像上的绝对中位差法 + 降噪 + 标记点浸染连线 + 图连通搜索
- numpy + 各种提速技巧
执行时间:
11秒
通过率:
一般
③因为耗时还是比较长,所以第三个版本主要还是对第二个版本的性能改进,主要是使用多进程分摊计算量,以达到加速计算的目的。
实现思路:
- BGR图像上的绝对中位差法 + 降噪 + 标记点浸染连线 + 图连通搜索
- numpy + 各种提速技巧
- 多进程并发计算
执行时间:
4.3秒
通过率:
一般
④第四个版本,我决定在第三个版本的基础上,将要检测的图像由BGR图像转为灰度图像,一方面可以减少计算量,另一方面也看能否获得更好地结果。
实现思路:
- BGR图像转灰度图像
- 灰度图像上的绝对中位差法 + 降噪 + 标记点浸染连线 + 图连通搜索
- numpy + 各种提速技巧
- 多进程并发计算
执行时间:
3.5秒
通过率:
略有提升
⑤第五个版本使用哈里斯角点检测算法,替换掉了绝对中位差法,在标记点的检测上效果良好,所以降噪的部分也不再需要了。借助于哈里斯角点检测算法的优异效果,方案的通过率有了显著提升。
实现思路:
- BGR图像转灰度图像
- 哈里斯角点检测 + 标记点浸染连线 + 图连通搜索
检测效果和耗时成正相关,通过阈值的调节,找一个比较合适的选择。
执行时间:
0.9秒
通过率:
100% (低样本数)
最终版本的方案我让朋友帮我测试过,共提交了100次,均成功通过,所以成功率100%?
这个样本数还是偏少了,不确定在1000次、10000次下是不是也能达到100%,但即便有偏差,应该也不会偏差太多。
来源:CSDN: https://blog.csdn.net/aaronjny/article/details/110245896